Core and affiliate faculty of the 2DCC can provide expertise in a wide range of physio-chemical aspects of two-dimensional materials growth, characterization, and properties. These efforts can be predictive – preceding associated experimental efforts, or interpretive – assisting in the understanding of existing experimental efforts. As a 2DCC User, you can request specific theory/simulation capabilities in your user proposal, or later as your project proceeds and new opportunities emerge, perhaps through interactions with 2DCC staff. We do have certain overall resource limitations, so access to a specific capability is dependent on availability of personnel and associated resources to support their work.

The Reactive Force Field known as ReaxFF1 is a framework for empirical atomistic dynamical simulations of growing materials, including chemical reactionsthat may take place in the gas phase or on the surface, for systems up to ~1,000,000 atoms and over timescales not accessible to first-principles techniques. The 2DCC makes extensive use of reactive force fields and continues to extend their application to more complex and realistic synthetic environments, with the codes hosted at the Penn State Material Computation Center. ReaxFF is supported in LAMMPS2 and can be used for molecular dynamics (NVE, NVT, NPT, μVT ensembles), energy minimization, Monte Carlo, hybrid Monte Carlo (i.e. Force Biased Monte Carlo3) and hyperdynamics/metadynamics acceleration methods such as Parallel Replica4,5, Parallel Tempering6, Collective Variable Hyperdynamics7 and Bond Boost Dynamics8,9.

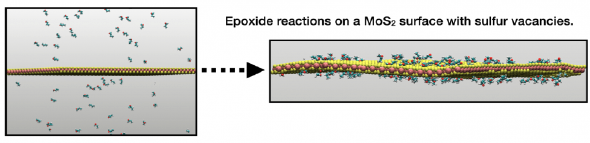Image of ReaxFF simulationSpecific implementations of ReaxFF are generally developed for each materials systems of interest, guided by and validated against a combination of first-principles and experimental data. Materials systems and substrates of potential interest to 2DCC users for which implementations currently exist include: 

  • MoS210,11
  • WSe2 (unpublished) 
  • Graphene + defects, including plasma treatment11,12
  • Plasma-assisted defect generation in graphene13
  • hBN (on metal surfaces)14,15
  • MXenes, specifically TiC16-19with a Mo extension under development
  • Phosphorene20
  • Silicene21-23
  • Sulfur (solid and molecular)24
  • Selenium (solid and molecular) (unpublished)
  • MoO3 (solid and molecular)25
  • Molecular precursors used in chemical vapor deposition: Mo(CO)6, W(CO)6, H2S, and H2Se
  • Hydrocarbon molecules (H/C/O)
  • Gallium and Indium metals, including interaction with Si.
  • GaN

If you would like access to these existing potentials above, please email: Adri van Duin at acv13@psu.edu 

For potentials not on the above list, please visit the research project proposal portal to submit a user proposal for potential development. Users are encouraged to discuss proposal ideas with Adri van Duin prior to submission. 

Reactive force fields are currently under development for MoSe2, WS2and associated alloy systems.  Certain substrates can also be simulated, including

  • SiO226
  • Al2O327
  • SiC28-29
  • Graphene, including defects and interactions with sulfur and MoS211

These substrates can be used for physicalinteractions with all 2D-materials. Reactiveinteractions between a substrate and growing 2D layer involve additional force field development. This level of theory is currently under development for  MoS2/SiO2, followed by extension to other Mo/W/Se/S phases and additional substrates.

Possible applications of ReaxFF to your synthesis efforts could include direct simulation of the complex kinetics involved at the substrate surface to guide the choice of substrate or growth conditions for MBE or CVD, chemical kinetics in the gas phase prior to arrival of species at the substrate to better inform choices of precursors for MOCVD, or simulation of interfacial reactivity in a heterostructure with any growth method. The computational efficiency of these methods enable the generation of very large datasets of complex kinetic phenomena that are then amenable to further analysis using machine learning methods. Non-reactive phenomena such as elastic response can also be accessed. 2DCC staff also have experience with registry-dependent interlayer potentials (of the Kolmogorov-Crespi form30) that can handle complex relaxations in e.g. twisted bilayers. Some of these applications may be clear at the advent of your user project, and others may only arise midstream through your project.

MOCVD is a complex highly coupled phenomenon, with many critical steps in synthesis potentially happening in the gas phase and further complex kinetics once the substrate gets involved. Physical and chemical phenomena occur across a wide range of length scales and time scales, from the macroscale flow of gases in the reactor chamber to the atomic-scale nucleation and growth of the 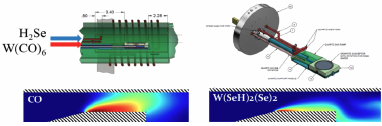MOCVD reactor schematic with CO and W(SeH)2Se2 concentration mapsresulting 2D material. 2DCC is developing a multi-scale computational approach which combines density functional calculations, reactive molecular dynamics, and full-scale computational fluid dynamics to better understand these processes30. The team is developing a detailed gas-phase chemical kinetic model to describe major chemical reaction pathways from precursors (for example, W(CO)6 and H2Se used to synthesize WSe2) to the thermodynamically stable end product, applying density functional theory to key gas-phase reactions to train and validate a ReaxFF force field that is then deployed to map out reaction pathways and energetics. Other kinetic parameters, plus thermal and transport properties of all species involved, are estimated from established kinetic/collisional theories.

This chemical kinetic model then informs computational fluid dynamics (CFD) simulations of gas-phase physio-chemical processes in the MOCVD chamber under experimental operating conditions, using a reacting flow solver31that captures gas-phase chemical reactions, gas-phase mass and heat transport, variable-density fluid dynamics, the transition from momentum-driven to buoyancy-driven flow, substrate rotation, and conjugate heat transfer. At this level of simulation, the CFD model can provide important insights into which reactive species actually impinge on the growth surface: these can vary dramatically from those injected into the chamber due to gas-phase reactions that proceed inhomogeneously as the reactants proceed through different physical conditions in their flow across the substrate. Parametric CFD simulations can determine the sensitivity of desired growth processes to operating conditions such as chamber pressure, substrate temperature, reactant injection speed, and reactant injection concentration. The team is currently focusing on gas-phase behavior for W(CO)6 and H2Se precursors in the growth of WSe2, and will extend to other systems as time and resources allow. Once chemical species contact the substrate, further complex chemistry ensues, with additional kinetic processes involved in transport of species along the substrate, at the growth edge, and on top of already-grown layers; these processes are currently being characterized for eventual integration with CFD models. Our intention is for high-fidelity theory and simulation to provide key insights to expand the scope of what is possible in terms of composition, doping, and material quality, with machine learning methods guiding the optimization to obtain desired growth outcomes.

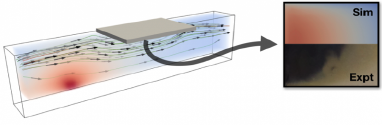Example of a computational cellSimilar methods can be applied to powder vapor transport growth of transition metal dichalcogenides, where the precise location of the substrate can have pronounced effects on the morphology of the resulting films, changing from isolated 2D islands, to a multigrain monolayer film, and vertical 2D materials.The 2DCC team can couple reactor-scale heat and mass transport equations with mesoscale phase-field equations for growth morphology considering the variation of edge energies with precursor concentration within the growth chamber to predict the spatial distributions of 2D islands32-35.

Example of kinetic parameter distributionPhase-field methods, currently under development, can describe island morphology evolution during growth of 2D materials taking into account the interplay of anisotropic edge energies, substrate/edge diffusivities, deposition rates and defect-island interactions. In these simulations, atomistic calculations provide information on edge energies, defect-island interactions and computational fluid dynamics simulations provide information on the initial precursor concentrations and deposition rates under different CVD growth conditions. Kinetic parameters such as diffusion barriers, adsorption energies and edge energies extracted from first-principles simulationscan also be fed into other larger-scale models such as kinetic Monte Carlo.

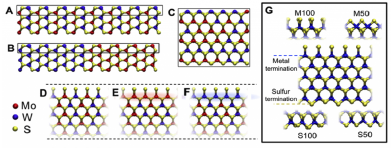Example of density functional methods outputDensity functional methods can provide the most accurate atomistic-level treatment of the relative energetics of different geometries that may be present during growth, and can also provide guidance on the relative thermodynamic stability of competing phases. Specific key geometries, defined through a combination of insights gleaned from experiment and empirical modeling, can be analyzed in great depth to identify viable candidates for microscopic mechanisms of key steps during growth. For example, metal atoms coordinated to vacancy defects in the substrate have been identified through first-principles modeling to potentially play a key role in lifting the near degeneracy between certain 180-degree misaligned polar domains on incommensurate polar substrates36. Experimental observation often inspire new calculations. For example, fascinating modulations in the composition within 2D layers (e.g. striping of Mo and W atoms within growing transition metal dichalcogenide monolayers) can motivate computational 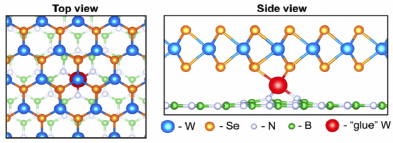Ball and stick model showing a W atom 'gluing' the 2D layer to the substrateinvestigations that reveal how fluctuations in the availability of chalcogenide at the growth edge can modulate the favorability to incorporate different metals, even when the bulk thermodynamics barely distinguishes the two species.

Image of MaterialsWeb.org logoThe 2DCC is partnering with MaterialsWeb.org to provide 2DCC users with detailed information on a comprehensive database of over 700 two-dimensional materials identified through high-throughput identification of low exfoliation energies from known bulk compounds37. The database currently provides the exfoliation energy, electronic band structure, and Pourbaix diagram for each material. The full database is freely available, and development is proceeding on extensions to incorporate defect energetics and other information on materials of specific interest to 2DCC users, integrated into the 2DCC user web access portal. Grand canonical genetic algorithm methods can further predict the composition and atomic structure of new 2D materials beyond those resident in the current database38. 

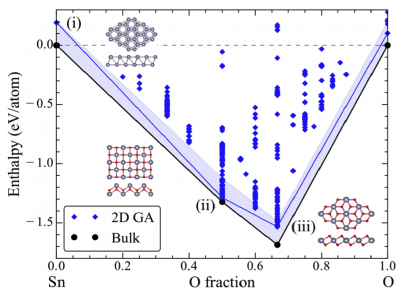Graph of Enthalpy vs O fraction for Sn-O for 2D GA and bulkExisting high-high-throughput databases are generally built around equilibrium or near-equilibrium thermodynamic properties of materials, while empirical methods handle more complex growth kinetics. The 2DCC team is pursuing high-throughput screening of optimal 2D material / substrate combinations by correlating key characteristics of kinetic growth models at the atomistic level39,40 with substrate/precursor interactions that can be derived from high-throughput models, to provide insights on the choice of substrate when growing a target material. Data-centric methods are also infused through the other theory/modeling capabilities described on this page – please refer to the other sections to learn more.

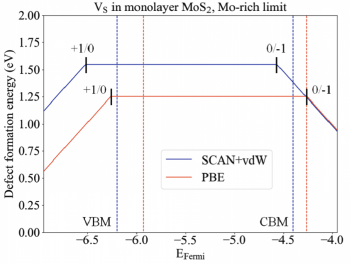Energy of defect formation versus Fermi Energy for Mo rich MoS2Electronic states associated with structural defects in 2D materials often dominate their optical response, limit the performance possible in electronic and optoelectronic applications, and impede the discernment of ideal characteristics and exotic quantum correlated phenomena at low temperature. Computations of such defects is particularly complex when they carry a non-zero charge. The formation energy must account for corrections due to electrostatic interactions with periodic images and compensating background charges in the vacuum which are introduced in supercell calculations; i.e. we must restores the appropriate electrostatic boundary conditions for charged 2D materials41. Properly corrected calculations can provide defect formation energies in 2D materials such as MoS2 and phosphorene, from which one can determine the charge transition levels, i.e., the positions of defect within the band gap. Detailed microscopic insights regarding specific defects can also be obtained from density functional calculations. For example, Jahn-Teller distortions can stabilize the charged states of chalcogenide vacancies in certain 2D materials by breaking the symmetry otherwise present between certain dorbitals. Furthermore, chemisorption of ligands to the surface of 2D layers can profoundly affect the ability to dope carriers into the layers, and the physisorption of various species is likewise strongly coupled to the charge state of the monolayer. Additional examples abound where carefully constructed first-principles methods provide insights into key aspects of experimental systems. The 2DCC team plans to develop an automated workflow to expedite the setup and post-processing of first-principles calculations of charged point defects in 2D materials and use it to create a new database of defect 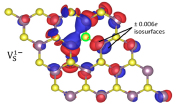Ball and stick model showing defect in MoS2properties in 2D and layered bulk materials. The development of this workflow will enable the rapid and robust evaluation of defect structures, formation energies, and electronic properties for different types of defects in a wide range of 2D materials.

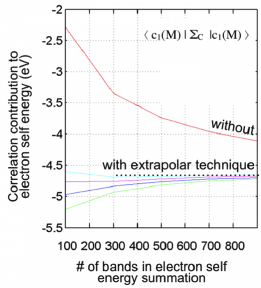Graph of correlation contribution to electron self energy versus number of bands in electron self energy summationThe 2DCC team can also model the excited state properties of pristine or defective 2D systems at the GW (including quasiparticle effects) and BSE levels (including excitonic effects). Using recently developed techniques42 that drastically accelerate convergence for GW calculations, we can extend these computationally demanding tasks to defective structures. In addition, time-dependent DFT methods parametrized from GW calculations43 can further accelerate excited-state calculations to enable the high-throughput screening of defect properties. Experimentally measured properties accessible to (potentially high-throughput) computation include optical absorption spectroscopy, electron energy loss spectroscopy, resonant or non-resonant Raman intensities, and second-order nonlinear susceptibility (second harmonic generation). This work is proceeding with partners at Cal State Northridge.

The 2DCC is supported by partnership with the Materials Computation Center (MCC) and the Institute for CyberScience – Advanced Cyberinfrastructure (ICS-ACI) at Penn State.

The MCC supports simulations of materials across multiple length and time scales, with technical support of advanced simulation software. The 2DCC is implementing, in partnership with the MCC, an integrated suite of software tools, hardware resources, and computational expertise to support direct simulation of key processes during materials growth, to suggest routes to overcome experimental obstacles, to assist in the interpretation of in situ characterization and post-synthesis measurement of samples, and also to predict new synthesis targets. 2DCC users will have access to MCC capabilities in computational methods including first-principles techniques at the density functional level (Quantum Espresso, VASP, etc.) and powerful empirical methods that can model complex reaction pathways over long time scales and length scales at both atomistic (ReaxFF) and phase-field levels.

One layer below MCC in the high-performance computation stack is the ICS-ACI, which acquires, hosts, and supports high-performance computational hardware and software. 2DCC computational resources will reside and be maintained by ICS-ACI. The ICS-ACI central facility serves the entire campus and is located at Penn State’s University Park Campus in the Penn State Data Center. The total computational resource of the ICS-ACI currently include:

  • Compute Resources - 23,000 basic-, standard- and high-memory nodes (128 GB, 256 GB, and 1 TB) with dual 10- or 12-core Xeon E5-2680 processors.
  • Storage - Over 2.5 PB of network-attached storage (NAS) to support users’ Home, Work, and Group storage needs and 2.5 PB of general parallel file system (GPFS) for Scratch storage in addition to 4 PB of tape storage for backup purposes. 
  • Network - High-performance Network Fabric built on Brocade VCS fabric technology. The architecture employs a research-centric software stack and customized environments allow researchers to deploy software from pre-compiled and tested software catalogs. The software stack supports both commercial and Opensource software.
  1. T.P. Senftle, S. Hong, M.M. Islam, S.B. Kylasa, Y. Zheng, Y.K. Shin, C. Junkermeier, R. Engel-Herbert, M.J. Janik, H.M. Aktulga, T. Verstraelen, A. Grama, and A.C.T. van Duin, «The reaxff reactive force-field: development, applications and future directions», Npj Computational Materials 2 (2016), p. 15011.
  2. S. Plimpton, «Fast parallel algorithms for short-range molecular dynamics», J. Comput. Phys. 117 (1995), pp. 1 – 19, 
  3. E.C. Neyts, Y. Shibuta, A.C.T. van Duin, and A. Bogaerts, «Catalyzed growth of carbon nanotube with definable chirality by hybrid molecular dynamicsforce biased monte carlo simulations», ACS Nano 4 (2010), pp. 6665–6672, 
  4. A.F. Voter, «Parallel replica method for dynamics of infrequent events», Phys. Rev. B 57 (1998), pp. R13985–R13988
  5. K.L. Joshi, S. Raman, and A.C.T. van Duin, «Connectivity-based parallel replica dy- namics for chemically reactive systems: From femtoseconds to microseconds», The Journal of Physical Chemistry Letters 4 (2013), pp. 3792–3797
  6. L. Atmani, C. Bichara, R.J.M. Pellenq, H. Van Damme, A.C.T. van Duin, Z. Raza, L.A. Truflandier, A. Obliger, P.G. Kralert, F.J. Ulm, and J.M. Leyssale, «From cellulose to kerogen: molecular simulation of a geological process», Chem. Sci. 8 (2017), pp. 8325–8335
  7. K.M. Bal and E.C. Neyts,«Merging metadynamics into hyperdynamics: Accelerated molecular simulations reaching time scales from microseconds to seconds», Journal of Chemical Theory and Computation 11 (2015), pp. 4545–4554
  8. T. Cheng, A. Jaramillo-Botero, W.A. Goddard, and H. Sun, «Adaptive accelerated reaxff reactive dynamics with validation from simulating hydrogen combustion», Journal of the American Chemical Society 136 (2014), p. 94349442
  9. A. Vashisth, C. Ashraf, W. Zhang, C.E. Bakis, and A.C.T. van Duin, «Accelerated reaxff simulations for describing the reactive cross-linking of polymers», The Journal of Physical Chemistry A 122 (2018), pp. 6633–6642
  10. A. Ostadhossein, A. Rahnamoun, Y. Wang, P. Zhao, S. Zhang, V.H. Crespi, and A.C.T. van Duin, «Reaxff reactive force-field study of molybdenum disulfide (mos2)», The Journal of Physical Chemistry Letters 8 (2017), pp. 631–640
  11. D.E. Yilmaz, R. Lotfi, C. Ashraf, S. Hong, and A.C.T. van Duin, «Defect design of two dimensional mos2 structures by using a graphene layer and potato stamp concept»,The Journal of Physical Chemistry C 122 (2018), pp. 11911–11917
  12. S.G. Srinivasan, A.C.T. van Duin, and P. Ganesh, «Development of a reaxff potential for carbon condensed phases and its application to the thermal fragmentation of a large fullerene», The Journal of Physical Chemistry A 119 (2015), pp. 571–580
  13. K. Yoon, A. Rahnamoun, J.L. Swett, V. Iberi, D.A. Cullen, I.V. Vlassiouk, A. Belianinov, S. Jesse, X. Sang, O.S. Ovchinnikova, A.J. Rondinone, R.R. Unocic, and A.C. van Duin, «Atomistic-scale simulations of defect formation in graphene u der noble gas ion irradiation», ACS Nano 10 (2016), pp. 8376–8384
  14. S. Liu, J. Comer, A.C.T. van Duin, D.M. van Duin, B. Liu, and J.H. Edgar, «Predicting the preferred morphology of hexagonal boron nitride domain structure on nickel from reaxff- based molecular dynamics simulations», Nanoscale 11 (2019), pp. 5607–5616
  15. S. Liu, A.C.T. van Duin, D.M. van Duin, B. Liu, and J.H. Edgar, «Atomistic insights into nucleation and formation of hexagonal boron nitride on nickel from first-principles-based reactive molecular dynamics simulations», ACS Nano 11 (2017), pp. 3585–3596
  16. N.C. Osti, M. Naguib, K. Ganeshan, Y.K. Shin, A. Ostadhossein, A.C.T. van Duin, Y. Cheng, L.L. Daemen, Y. Gogotsi, E. Mamontov, and A.I. Kolesnikov, «Influence of metal ions intercalation on the vibrational dynamics of water confined between mxene layers», Phys. Rev. Materials 1 (2017), p. 065406
  17. N.C. Osti, M. Naguib, A. Ostadhossein, Y. Xie, P.R.C. Kent, B. Dyatkin, G. Rother, W.T. Heller, A.C.T. van Duin, Y. Gogotsi, and E. Mamontov, «Effect of metal ion intercalation on the structure of mxene and water dynamics on its internal surfaces», ACS Applied Materials & Interfaces 8 (2016), pp. 8859–8863
  18. X. Sang, Y. Xie, D.E. Yilmaz, R. Lotfi, M. Alhabeb, A. Ostadhossein, B. Anasori, W. Sun, X. Li, K. Xiao, P.R.C. Kent, A.C.T. van Duin, Y. Gogotsi, and R.R. Unocic, «In situ atomistic insight into the growth mechanisms of single layer 2d transition metal carbides», Nature Communications 9 (2018), p. 2266.
  19. R. Lotfi, M. Naguib, D.E. Yilmaz, J. Nanda, and A.C.T. van Duin, «A comparative study on the oxidation of two-dimensional ti3c2 mxene structures in different environments», J. Mater. Chem. A 6 (2018), pp. 12733–12743
  20. H. Xiao, X. Shi, F. Hao, X. Liao, Y. Zhang, and X. Chen, «Development of a transferable reactive force field of p/h systems: Application to the chemical and mechanical properties of phosphorene», The Journal of Physical Chemistry A 121 (2017), pp. 6135–6149
  21. G.R. Berdiyorov, M. Neek-Amal, F.M. Peeters, and A.C.T. van Duin, «Stabilized silicene within bilayer graphene: A proposal based on molecular dynamics and density-functional tight binding calculations», Phys. Rev. B 89 (2014), p. 024107
  22. T. Botari, E. Perim, P.A.S. Autreto, A.C.T. van Duin, R. Paupitz, and D.S. Galvao, «Mechanical properties and fracture dynamics of silicene membranes», Phys. Chem. Chem. Phys. 16 (2014), pp. 19417–19423
  23. G.R. Berdiyorov and F.M. Peeters, «Influence of vacancy defects on the thermal stability of silicene: a reactive molecular dynamics study», RSC Adv. 4 (2014), pp. 1133–1137
  24. M.M. Islam, A. Ostadhossein, O. Borodin, A.T. Yeates, W.W. Tipton, R.G. Hennig, N. Kumar, and A.C.T. van Duin, «Reaxff molecular dynamics simulations on lithiated sulfur cathode materials», Phys. Chem. Chem. Phys. 17 (2015), pp. 3383–3393
  25. K. Chenoweth, A. vanDuin, and W. Goddard III, «The reaxff monte carlo reactive dynamics method for predicting atomistic structures of disordered ceramics: Application to the mo3vox catalyst», Angewandte Chemie International Edition 48 (2009), pp. 7630–7634. 
  26. M.C. Pitman and A.C.T. van Duin, «Dynamics of confined reactive water in smectite clayzeolite composites», Journal of the American Chemical Society 134 (2012), pp. 3042– 3053
  27. F.A. Soria, W. Zhang, P.A. Paredes-Olivera, A.C.T. van Duin, and E.M. Patrito, «Si/c/h reaxff reactive potential for silicon surfaces grafted with organic molecules», The Journal of Physical Chemistry C 122 (2018), pp. 23515–23527
  28. F.A. Soria, W. Zhang, A.C.T. van Duin, and E.M. Patrito, «Thermal stability of organic monolayers grafted to si(111): Insights from reaxff reactive molecular dynamics simulations», ACS Applied Materials & Interfaces 9 (2017), pp. 30969–30981
  29. A.N. Kolmogorov and V.H. Crespi, «Registry-dependent interlayer potential for graphitic systems», Phys. Rev. B 71 (2005), p. 235415
  30. A. Jain, S. Zafar, R. Lotfi, N. Nayir, Y. Wang, T. Choudhury, J. Redwing, V. Crespi, Y. Xuan, and A. van Duin, «Development of a reaxff reactive force field for w/se/c/o/h systems and its application to a gas-phase chemical kinetic mechanism for w(co)6/h2se mixtures using a multi-scale approach», (Unpublished work).
  31. B. Savard, Y. Xuan, B. Bobbitt, and G. Blanquart, «A computationally-efficient, semi-implicit, iterative method for the time-integration of reacting flows with stiff chemistry», J. Comput. Phys. 295 (2015), pp. 740–769
  32. R.A. Vila, K. Momeni, Q. Wang, B.M. Bersch, N. Lu, M.J. Kim, L.Q. Chen, and J.A. Robinson, «Bottom-up synthesis of vertically oriented two-dimensional materials», 2D Materials 3 (2016), p. 041003.
  33. F. Zhang, K. Momeni, M.A. AlSaud, A. Azizi, M.F. Hainey, J.M. Redwing, L.Q. Chen, and N. Alem, «Controlled synthesis of 2d transition metal dichalcogenides: from vertical to planar MoS2», 2D Materials 4 (2017), p. 025029.
  34. N. Briggs, S. Subramanian, Z. Lin, X. Li, X. Zhang, K. Zhang, K. Xiao, D. Geohegan, R. Wallace, L.Q. Chen, M. Terrones, A. Ebrahimi, S. Das, J. Redwing, C. Hinkle, K. Momeni, A. van Duin, V. Crespi, S. Kar, and J.A. Robinson, «A roadmap for electronic grade 2d materials», 2D Materials 6 (2019), p. 022001.
  35. K. Momeni, Y. Ji, K. Zhang, J.A. Robinson, and L.Q. Chen, «Multiscale framework for simulation-guided growth of 2d materials», npj 2D Materials and Applications 2 (2018), pp. 2397–7132.
  36. X. Zhang, F. Zhang, Y. Wang, D.S. Schulman, T. Zhang, A. Bansal, N. Alem, S. Das, V.H. Crespi, M. Terrones, and J.M. Redwing,«Defect-controlled nucleation and orientation of wse2 on hbn: A route to single-crystal epitaxial monolayers», ACS Nano 13 (2019), pp. 3341–3352, Available at https://doi.org/10.1021/acsnano.8b09230, pMID: 30758945.
  37. M. Ashton, J. Paul, S.B. Sinnott, and R.G. Hennig, «Topology-scaling identification of layered solids and stable exfoliated 2d materials», Phys. Rev. Lett. 118 (2017), p. 106101,
  38. A.K. Singh, B.C. Revard, R. Ramanathan, M. Ashton, F. Tavazza, and R.G. Hennig, «Genetic algorithm prediction of two-dimensional group-iv dioxides for dielectrics», Phys. Rev. B 95 (2017), p. 155426
  39. Z. Zhang, Y. Liu, Y. Yang, and B.I. Yakobson, «Growth mechanism and morphology of hexagonal boron nitride», Nano Letters 16 (2016), pp. 1398–1403
  40. A. Govind Rajan, J.H. Warner, D. Blankschtein, and M.S. Strano, «Generalized mechanistic model for the chemical vapor deposition of 2d transition metal dichalcogenide monolayers», ACS Nano 10 (2016), pp. 4330–4344, pMID: 26937889.
  41. C. Freysoldt and J. Neugebauer, «First-principles calculations for charged defects at surfaces, interfaces, and two-dimensional materials in the presence of electric fields», Phys. Rev. B 97 (2018), p. 205425
  42. F. Bruneval and X. Gonze, «Accurate gw self-energies in a plane-wave basis using only a few empty states: Towards large systems», Phys. Rev. B 78 (2008), p. 085125.
  43. L.y. Huang, X. Zhang, M. Zhang, and G. Lu, «Effect of point defects on optical properties of graphene fluoride: A first-principles study», The Journal of Physical Chemistry C 121 (2017), pp. 12855–12862.